| 10 | 2024/11 | 12 |
| S | M | T | W | T | F | S |
|---|---|---|---|---|---|---|
| 1 | 2 | |||||
| 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| 17 | 18 | 19 | 20 | 21 | 22 | 23 |
| 24 | 25 | 26 | 27 | 28 | 29 | 30 |
10/01/10 1:45最終更新
間違いを訂正致しました。申し訳ありませんでした＞_＜
雨さんご指摘どうもありがとうございます。
勝ちに直結する崩しパターンが発動するための必要攻撃回数を比較する
ことで比較的簡単に行うことができると思います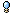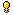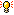
相手を崩すのに必要な攻撃回数＝相手が耐えられる流し回数
と捉えてももちろんいいです。
そしてその必要攻撃回数が少なければ少ないほど速い決定力ということにっ
とりあえず簡単のために急所は無視しちゃいましょう。
また、以下の攻撃は原則、流し合いのサイクルの中で当て逃げを繰り返した場合を考えています。
①命中率100％の技で確定n発で倒せる場合
これが1番簡単です！
例えば「55カビゴンの捨身タックルで50持ち物なしカイリキーを倒す」パターンに必要な攻撃回数は
命中率100％の捨身タックルで確定2発なので2回です。
②端的な攻撃回数で量れない場合
確率を攻撃回数の次元に落とす必要がありますよね。「55ケンタロスのつのドリルで55カイリキーを倒す」パターンの必要攻撃回数は
そのパターンの確率の逆数が必要攻撃回数に相当します。
確率0.3の逆数をとって3.33回。1.96回 ③と同様に計算します
確率0.7x0.3=0.21の逆数をとって4.76回。
「パルシェンの冷凍ビームで奇跡の実スターミーに凍結が入る」パターンの必要攻撃回数は
確率0.1の逆数10回に奇跡の実の影響で10回x2＝20回となります。
蛇足ですが、、
巨視的に見れば一撃技はあらゆるポケモンに対して乱数3発の技を放っていることと同義であると言えます。
以上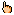
が基本の計算方法。以下
は応用です。
③命中率p％の技で確定n発で倒せる場合
たとえば50カビゴンの大文字で50パルシェンは確定3発。
しかし当然大文字は15％の確率で外れてしまうので必ず3発で倒せるとは限りません。
この場合の必要攻撃回数は以下のように計算します。
重要なのは逆に攻撃回数を確率の次元に落とすことです。
・3回で倒せる場合
3回で倒す確率＝0.85＾3＝0.614
攻撃回数に相当する確率＝3回の逆数＝0.333
従って3回で倒すための必要攻撃回数に相当する確率＝0.614x0.333＝0.205
・4回で倒せる場合
きっかり4回で倒す確率＝(0.85^3x0.15^1)x3＝0.276
攻撃回数に相当する確率＝4回の逆数＝0.25
従って4回で倒すための必要攻撃回数に相当する確率＝0.276x0.25＝0.0691
・5回で倒せる場合
きっかり5回で倒す確率＝(0.85^3x0.15^2)x6＝0.0829
攻撃回数に相当する確率＝5回の逆数＝0.2
従って5回で倒すための必要攻撃回数に相当する確率＝0.0829x0.2＝0.0166
この操作をＰＰの切れる8回まで繰り返すのが理想的ですが、、
さすがに気が引けちゃう。。
なので3つくらいまで場合分け（今回は3～5回まで）すれば十分かなってooo
最後に確率の和＝0.205+0.0691+0.00166＝0.290の逆数をとって約3.4回。
これが50カビゴンが大文字で50パルシェンを倒す必要攻撃回数となります。
④命中率100％の技で乱数n発で倒せる場合
それぞれどのくらいの確率でn発、n+1発なのかを見積もることができれば
③と同様にして必要攻撃回数を求めることができます。
⑤命中率p％の技で乱数n発で倒せる場合
これも今までの応用ですよね。
⑥リスクを伴うパターンの場合
当て逃げでなくお互いに攻撃を打ち合うパターンを考えるときは
当然ですけど相手の攻撃も考慮する必要があります。
例えば「50パルシェンで雷を交わして50サンダーを爆発で倒す」パターンの必要攻撃回数は
雷の外れる確率0.3の逆数をとって3.33回ですが、
同時に雷の命中する70％の負けを背負っているので
無条件に相手側に必要攻撃回数1.46回の決定力を与えてしまうことになります。（ただしパルシェンを一方的に失っても負け確定でない場合は別です。）
⑦読みが絡むパターンの場合
ここまで「～読み」という行動は一切排除しして考えてきましたけど、、
読みが絡む場合も読みを確率と捉えることで解決します。
上記と同じように読みの成功率とその後の崩しパターンの確率の積をとって逆数をとります。
これらのことを踏まえると、どちらのパーティが早く決定力が出せるかというシミュレーションを割と楽に行うことができそうです
また、不利な側はどのように立ち回ればいいのかも見えてくる場合があります。
たとえば簡単な例として
サトシがシゲルを崩す最速の崩しパターンの攻撃回数が4.5回で
シゲルがサトシを崩す最速の崩しパターンの攻撃回数5.0回である場合、
シゲルは1回危険な読みを成功させることで1回攻撃回数が減って4.0回となるので
それを目標に立ち回る必要性が出て来る、ということが分かります。
もちろんこの量り方は万能ではありませんが、対戦のアウトラインを知りたいときには十分です。
次回以降の更新では具体的な2vs2と3vs3をシミュレーションしてみたいと思います
おおぅ、これはすごいですね＞＜
とても、参考になります。
大まかな速度計算しかしたことがない
＆速度の計算方法を厳密に考えたことが無かった
ので、今度この方法を使わせてもらおうかなぁと思いました。
という驚きから、思わずコメントしてしまいました（笑
で、さっそく質問なんですけれど
命中率や乱数の絡む攻撃回数を求める時は
X回で確実に落せる確率を1/Xとして
そこから命中率や乱数の確率があるので
1/Xから命中率と乱数分の確率が減ると考えるのであってますか？＞＜
（↑だと従って5回で倒すための必要攻撃回数に相当する確率＝0.0829x0.2＝0.0166の部分かな。）
ってことは
急所、乱数、命中率も含めてX回の攻撃回数においてYの確率で落せるっていうのを求めれば
1/X×YをしてX+1回のとき、X-1回のとき～ってすべての厳密な確率を求めて
それらを足して逆数を取れば
急所も含めた厳密な攻撃回数が出せる…であっていますか？＞＜
今度、本気で計算してみようと思いました。
なんか日本語下手なのでわかりにくくなったかも＞＜
あ、今年もよろしくお願いします＞＜（遅
一撃必殺の必要回数に関して少々疑問が湧いたので、私なりの意見を纏めてみました。
・ケンタロス(角ドリル所持)/何か/何か
・カビゴン(捨て身タックル所持)/何か/何か
のパーティーが対戦した場合を想定します。
・ケンタロス側の最速の崩しパターンは、カビゴン側のケンタロス受けを「角ドリル」で倒すこと
・カビゴン側の最速の崩しパターンは、ケンタロス側のカビゴン受けをカビゴンの「捨て身タックル」で倒すこと
と仮定します。この時
・ケンタロス側の必要攻撃回数は3.3回(レベル差による命中率の補正は無視します；)
・カビゴン側の必要攻撃回数は３回
と仮定します。
流し合いのサイクルの中で交互に当て逃げする、という想定をすると
①ケンタロスが最初に「流し」を行った場合
カビゴンが必要攻撃回数３をカウントする前に、ケンタロスが「角ドリル」を打つことが出来る回数は２回
→ケンタロス側が先にケンタロス受けを突破する確率は51％
②カビゴン側が最初に「流し」を行った場合
カビゴン側が必要攻撃回数３をカウントする前に、ケンタロスが「角ドリル」を打つことが出来る回数は３回
→ケンタロス側が先にケンタロス受けを突破する確率は65.7％
①と②が発生する確率は読み合いで決まるので一概には言えませんが、どちらにせよケンタロス側は攻撃回数を減らす読みをせずとも、50％以上の確率で先に決定力を発揮できます。
一般的な技は命中率が高いため、分散がさほど大きくならないのでこの計算方法で比較できそうですが、一撃必殺のように分散の大きな技に関しては、あまり当てはまらないのではないかと思いました。
仮定だらけの上ケチをつける様で済みません； ですがほとんどの技に関してはこの方法で比較できそうなので、自分のパーティーを構築する際にも試してみようと思います。
コメントありがとうございます！
こちらこそ今年もどうぞよろしくお願いいたしますねっ♪
>>命中率や乱数の絡む攻撃回数を求める時は
X回で確実に落せる確率を1/Xとして
そこから命中率や乱数の確率があるので
1/Xから命中率と乱数分の確率が減ると考えるのであってますか？＞＜
（↑だと従って5回で倒すための必要攻撃回数に相当する確率＝0.0829x0.2＝0.0166の部分かな。）
ってことは
急所、乱数、命中率も含めてX回の攻撃回数においてYの確率で落せるっていうのを求めれば
1/X×YをしてX+1回のとき、X-1回のとき～ってすべての厳密な確率を求めて
それらを足して逆数を取れば
急所も含めた厳密な攻撃回数が出せる…であっていますか？＞＜
ぇっと、たぶんあっていると思います☆
けれどＸから離れるに従って回数への寄与はものすごく小さくなっていくので
そこまで厳密な場合分けをしなくとも目安の値は求まると思います！
＞雨さん
ここでは初めましてです☆
コメント、心より感謝申し上げますｍｍ
ぇっと、、
本当にごめんなさい。。
一撃技を単純に0.3の逆数で扱うのはまずかったです；≧ω≦
そして同様に②のサンダーの麻痺やパルシェン凍結についてもこれではまずいですね。
訂正しないと。。
分散の寄与も考慮するには
やっぱり大文字みたいに場合分けする必要があるってことかな。。
とりあえず一撃技を考えると、
・1回で倒す場合
パターンの確率＝0.3
攻撃回数相当の確率＝1
よってこの場合の確率＝1x0.3=0.3
・2回で倒す場合
パターンの確率＝0.7x0.3＝0.21
攻撃回数相当の確率＝0.5
よってこの場合の確率＝0.21x0.5=0.105
これを8回繰り返して和をとると確率0.511
逆数をとると約1.96回。
こちらなら正しいでしょうか???
必要回数2回の相手には分が悪く3回の相手には有利なので、一撃必殺技の必要回数が求められるのならば２～３の間になるのではないでしょうか？
具体的な計算方法等は指摘できませんが；
引き続きコメントを頂きまして誠にありがとうございます☆
雨さんがおっしゃってくださっているのは、、
雨さんの先日のケンタロスvsカビゴンのシミュレーションをお借りすると
ケンタロス側の最速崩しパターン：つのドリルでケンタ受けを倒す。必要攻撃回数1.96回
カビゴン側の最速崩しパターン：捨身タックルでカビ受けを倒す。必要攻撃回数2回
としたときに
ケンタロスが先に受ける場合：ケンタロス側の勝率30％
カビゴンが先に受ける場合：ケンタロス側の勝率51％
となって微々たる必要攻撃回数の差にそぐわないほどの勝率の差が生まれて
カビゴン側有利、ってことですよね！？
おっしゃるとおりだと思います；
ごめんなさい、だとするとまた次なる訂正が求められちゃいますね；
あの...ここからは完全に私の憶測なんですけども、、
カビゴン側の必要攻撃回数が2回のとき
→ケンタロスは理論上最高でも2発しかつのドリルを打てない
→PP8回分までの総和をとる（＝1.96回）のは間違い；；
→攻撃回数はPP1～2回分に相当、必要攻撃回数3.33～2.47回の間
カビゴン側の必要攻撃回数が3回のとき
→ケンタロスは理論上最高でも3発しかつのドリルを打てない
→PP8回分までの総和をとるのは間違い；；
→攻撃回数はPP2～3回分に相当、必要攻撃回数2.47～2.22回の間
このように考えるとしっくりくるんですけど。。
当っているようで、でもこじつけっぽくも見えて悩み中です；≧ω≦
もしそうだとすると今回のようにカビゴン側が確定2発という明確な値が得られている場合はいいのですが、、
両者の崩しパターンが一撃技のようなPP回数に依存する必要攻撃回数の場合、シミュレーションをするのは困難を極めることに???
明確なお答えができなくてごめんなさいです。
もうちょっと深く考えてみたいと思います！
[PR]